Introduction to Deep Learning in Python
This is the memo of the 25th course of ‘Data Scientist with Python’ track.
You can find the original course HERE .
1. Basics of deep learning and neural networks
1.1 Introduction to deep learning



1.2 Forward propagation

Coding the forward propagation algorithm
In this exercise, you’ll write code to do forward propagation (prediction) for your first neural network:
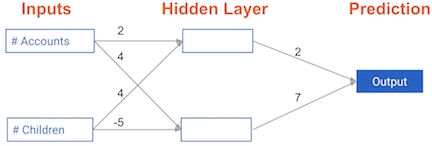
Each data point is a customer. The first input is how many accounts they have, and the second input is how many children they have. The model will predict how many transactions the user makes in the next year.
You will use this data throughout the first 2 chapters of this course.
It looks like the network generated a prediction of -39 .
1.3 Activation functions



The Rectified Linear Activation Function
An “activation function” is a function applied at each node. It converts the node’s input into some output.
The rectified linear activation function (called ReLU ) has been shown to lead to very high-performance networks. This function takes a single number as an input, returning 0 if the input is negative, and the input if the input is positive.
Here are some examples:
relu(3) = 3
relu(-3) = 0
You predicted 52 transactions. Without this activation function, you would have predicted a negative number!
The real power of activation functions will come soon when you start tuning model weights.
Applying the network to many observations/rows of data
1.4 Deeper networks


Forward propagation in a deeper network
You now have a model with 2 hidden layers. The values for an input data point are shown inside the input nodes. The weights are shown on the edges/lines. What prediction would this model make on this data point?
Assume the activation function at each node is the identity function . That is, each node’s output will be the same as its input. So the value of the bottom node in the first hidden layer is -1, and not 0, as it would be if the ReLU activation function was used.
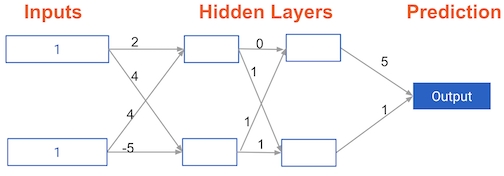
| Hidden Layer 1 | Hidden Layer 2 | Prediction | | 6 | -1 | | | | | 0 | | -1 | 5 | |
Multi-layer neural networks
In this exercise, you’ll write code to do forward propagation for a neural network with 2 hidden layers. Each hidden layer has two nodes.
Representations are learned
How are the weights that determine the features/interactions in Neural Networks created?
The model training process sets them to optimize predictive accuracy.
Levels of representation
Which layers of a model capture more complex or “higher level” interactions?
The last layers capture the most complex interactions.
2. Optimizing a neural network with backward propagation
2.1 The need for optimization
Calculating model errors
What is the error (predicted – actual) for the following network when the input data is [3, 2] and the actual value of the target (what you are trying to predict) is 5?

prediction = (3_2 + 2_1) _2 + (3_0 + 2_0)_2
=16
error = 16 – 5 = 11
Understanding how weights change model accuracy
Imagine you have to make a prediction for a single data point. The actual value of the target is 7. The weight going from node_0 to the output is 2, as shown below.
If you increased it slightly, changing it to 2.01, would the predictions become more accurate, less accurate, or stay the same?

prediction_before = 16
error_before = 16 – 7 = 9
prediction_after = (3_2.01 + 2_1) _2 + (3_0 + 2_0)_2
=16.x
error_after = 9.x
Increasing the weight to 2.01 would increase the resulting error from 9 to 9.08 , making the predictions less accurate.
Coding how weight changes affect accuracy
Now you’ll get to change weights in a real network and see how they affect model accuracy!
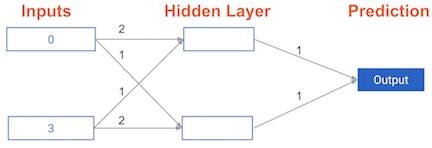
Have a look at the following neural network:
Its weights have been pre-loaded as weights_0 . Your task in this exercise is to update a single weight in weights_0 to create weights_1 , which gives a perfect prediction (in which the predicted value is equal to target_actual : 3).
Scaling up to multiple data points
You’ve seen how different weights will have different accuracies on a single prediction. But usually, you’ll want to measure model accuracy on many points.
You’ll now write code to compare model accuracies for two different sets of weights, which have been stored as weights_0 and weights_1 .
It looks like model_output_1 has a higher mean squared error.
2.2 Gradient descent


ex. learning rate = 0.01

w.r.t. = with respect to


new weight = 2 – -24 * 0.01 = 2.24
Calculating slopes
You’re now going to practice calculating slopes.
When plotting the mean-squared error loss function against predictions, the slope is 2 * x * (y-xb) , or 2 * input_data * error .
Note that x and b may have multiple numbers ( x is a vector for each data point, and b is a vector). In this case, the output will also be a vector, which is exactly what you want.
You’re ready to write the code to calculate this slope while using a single data point.
You can now use this slope to improve the weights of the model!
Improving model weights
You’ve just calculated the slopes you need. Now it’s time to use those slopes to improve your model.
If you add the slopes to your weights, you will move in the right direction. However, it’s possible to move too far in that direction.
So you will want to take a small step in that direction first, using a lower learning rate, and verify that the model is improving.
Updating the model weights did indeed decrease the error!
Making multiple updates to weights
You’re now going to make multiple updates so you can dramatically improve your model weights, and see how the predictions improve with each update.

As you can see, the mean squared error decreases as the number of iterations go up.
2.3 Back propagation
The relationship between forward and backward propagation
If you have gone through 4 iterations of calculating slopes (using backward propagation) and then updated weights.
How many times must you have done forward propagation?
4
Each time you generate predictions using forward propagation, you update the weights using backward propagation.
Thinking about backward propagation
If your predictions were all exactly right, and your errors were all exactly 0, the slope of the loss function with respect to your predictions would also be 0.
In that circumstance, the updates to all weights in the network would also be 0.
2.4 Backpropagation in practice

slope = 2 imput error

6 and 18 are slopes just calculated in the above graph


x <= 0: slope = 0
x > 0: slope = 1

gradient = input(white) slope(red) ReLU_slope(=1 here)
gradient_0 = 0_6_1 = 0
gradient_3 = 1_18_1 = 18
A round of backpropagation
In the network shown below, we have done forward propagation, and node values calculated as part of forward propagation are shown in white.
The weights are shown in black.
Layers after the question mark show the slopes calculated as part of back-prop, rather than the forward-prop values. Those slope values are shown in purple.
This network again uses the ReLU activation function, so the slope of the activation function is 1 for any node receiving a positive value as input.
Assume the node being examined had a positive value (so the activation function’s slope is 1).
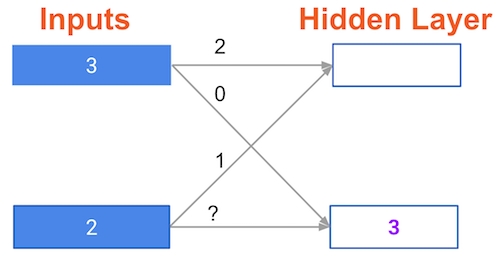
What is the slope needed to update the weight with the question mark?

gradient = input(white) slope(purple) ReLU_slope(=1 here)
= 2_3_1 = 6
3. Building deep learning models with keras
3.1 Creating a keras model

Understanding your data
You will soon start building models in Keras to predict wages based on various professional and demographic factors.
Before you start building a model, it’s good to understand your data by performing some exploratory analysis.
Specifying a model
Now you’ll get to work with your first model in Keras, and will immediately be able to run more complex neural network models on larger datasets compared to the first two chapters.
To start, you’ll take the skeleton of a neural network and add a hidden layer and an output layer. You’ll then fit that model and see Keras do the optimization so your model continually gets better.
Now that you’ve specified the model, the next step is to compile it.
3.2 Compiling and fitting a model
Compiling the model
You’re now going to compile the model you specified earlier. To compile the model, you need to specify the optimizer and loss function to use.
The Adam optimizer is an excellent choice. You can read more about it as well as other keras optimizers here , and if you are really curious to learn more, you can read the original paper that introduced the Adam optimizer.
In this exercise, you’ll use the Adam optimizer and the mean squared error loss function. Go for it!
Fitting the model
You now know how to specify, compile, and fit a deep learning model using keras!
3.3 Classification models
Understanding your classification data
Now you will start modeling with a new dataset for a classification problem. This data includes information about passengers on the Titanic.
You will use predictors such as age , fare and where each passenger embarked from to predict who will survive. This data is from a tutorial on data science competitions . Look here for descriptions of the features.
Last steps in classification models
You’ll now create a classification model using the titanic dataset.
Here, you’ll use the 'sgd' optimizer, which stands for Stochastic Gradient Descent . You’ll now create a classification model using the titanic dataset.
This simple model is generating an accuracy of 68!
3.4 Using models

Making predictions
In this exercise, your predictions will be probabilities, which is the most common way for data scientists to communicate their predictions to colleagues.
You’re now ready to begin learning how to fine-tune your models.
4. Fine-tuning keras models
4.1 Understanding model optimization
Diagnosing optimization problems
All of the following could prevent a model from showing an improved loss in its first few epochs.
Learning rate too low.
Learning rate too high.
Poor choice of activation function.
Changing optimization parameters
It’s time to get your hands dirty with optimization. You’ll now try optimizing a model at a very low learning rate, a very high learning rate, and a “just right” learning rate.
You’ll want to look at the results after running this exercise, remembering that a low value for the loss function is good.
For these exercises, we’ve pre-loaded the predictors and target values from your previous classification models (predicting who would survive on the Titanic).
You’ll want the optimization to start from scratch every time you change the learning rate, to give a fair comparison of how each learning rate did in your results. So we have created a function get_new_model() that creates an unoptimized model to optimize.
4.2 Model validation
Evaluating model accuracy on validation dataset
Now it’s your turn to monitor model accuracy with a validation data set. A model definition has been provided as model . Your job is to add the code to compile it and then fit it. You’ll check the validation score in each epoch.
Early stopping: Optimizing the optimization
Now that you know how to monitor your model performance throughout optimization, you can use early stopping to stop optimization when it isn’t helping any more. Since the optimization stops automatically when it isn’t helping, you can also set a high value for epochs in your call to .fit() .
Because optimization will automatically stop when it is no longer helpful, it is okay to specify the maximum number of epochs as 30 rather than using the default of 10 that you’ve used so far. Here, it seems like the optimization stopped after 7 epochs.
Experimenting with wider networks
Now you know everything you need to begin experimenting with different models!
A model called model_1 has been pre-loaded. You can see a summary of this model printed in the IPython Shell. This is a relatively small network, with only 10 units in each hidden layer.
In this exercise you’ll create a new model called model_2 which is similar to model_1 , except it has 100 units in each hidden layer.

The blue model is the one you made, the red is the original model. Your model had a lower loss value, so it is the better model.
Adding layers to a network
You’ve seen how to experiment with wider networks. In this exercise, you’ll try a deeper network (more hidden layers).

4.3 Thinking about model capacity



Experimenting with model structures
You’ve just run an experiment where you compared two networks that were identical except that the 2nd network had an extra hidden layer.
You see that this 2nd network (the deeper network) had better performance. Given that, How to get an even better performance?
Increasing the number of units in each hidden layer would be a good next step to try achieving even better performance.
4.4 Stepping up to images

Building your own digit recognition model
You’ve reached the final exercise of the course – you now know everything you need to build an accurate model to recognize handwritten digits!
To add an extra challenge, we’ve loaded only 2500 images, rather than 60000 which you will see in some published results. Deep learning models perform better with more data, however, they also take longer to train, especially when they start becoming more complex.
If you have a computer with a CUDA compatible GPU, you can take advantage of it to improve computation time. If you don’t have a GPU, no problem! You can set up a deep learning environment in the cloud that can run your models on a GPU. Here is a blog post by Dan that explains how to do this – check it out after completing this exercise! It is a great next step as you continue your deep learning journey.
Ready to take your deep learning to the next level? Check out Advanced Deep Learning with Keras in Python to see how the Keras functional API lets you build domain knowledge to solve new types of problems. Once you know how to use the functional API, take a look at “Convolutional Neural Networks for Image Processing” to learn image-specific applications of Keras.
You’ve done something pretty amazing. You should see better than 90% accuracy recognizing handwritten digits, even while using a small training set of only 1750 images!
The End.
Thank you for reading.
Last updated
Was this helpful?






